Fluid flow is characterized by a velocity vector field in three-dimensional space, within the framework of continuum mechanics. Streamlines, streaklines and pathlines are field lines resulting from this vector field description of the flow. They differ only when the flow changes with time: that is, when the flow is not steady.
- Streamlines are a family of curves that are instantaneously tangent to the velocity vector of the flow. These show the direction a fluid element will travel in at any point in time.
- Streaklines are the locus of points of all the fluid particles that have passed continuously through a particular spatial point in the past. Dye steadily injected into the fluid at a fixed point extends along a streakline. These can be thought of as a "recording" of the path a fluid element in the flow takes over a certain period. The direction the path takes will be determined by the streamlines of the fluid at each moment in time.
- Pathlines are the trajectories that individual fluid particles follow.
- Timelines are the lines formed by a set of fluid particles that were marked at a previous instant in time, creating a line or a curve that is displaced in time as the particles move.
By definition, different streamlines at the same instant in a flow do not intersect, because a fluid particle cannot have two different velocities at the same point. Similarly, streaklines cannot intersect themselves or other streaklines, because two particles cannot be present at the same location at the same instant of time; unless the origin point of one of the streaklines also belongs to the streakline of the other origin point. However, pathlines are allowed to intersect themselves or other pathlines (except the starting and end points of the different pathlines, which need to be distinct).
Streamlines and timelines provide a snapshot of some flowfield characteristics, whereas streaklines and pathlines depend on the full time-history of the flow. However, often sequences of timelines (and streaklines) at different instants—being presented either in a single image or with a video stream—may be used to provide insight in the flow and its history.
A region bounded by streamlines is called a streamtube. In a steady flow—because the streamlines are tangent to the flow velocity—fluid that is inside a stream tube must remain forever within that same stream tube. A scalar function whose contour lines define the streamlines is known as the stream function.
Dye line may refer either to a streakline: dye released gradually from a fixed location during time; or it may refer to a timeline: a line of dye applied instantaneously at a certain moment in time, and observed at a later instant.
Streamlines
with "×" denoting the vector cross product and 
is the parametric representation of just one streamline at one moment in time.
If the components of the velocity are written 
and those of the streamline as 
we deduce:
which shows that the curves are parallel to the velocity vector. Here s is a variable which parametrizes the curve 
Streamlines are calculated instantaneously, meaning that at one instance of time they are calculated throughout the fluid from the instantaneous flow velocity field.
Pathlines
Pathlines are defined by
![\begin{cases} \displaystyle \frac{d\vec{x}_P}{dt} = \vec{u}_P(\vec{x}_P,t) \\[1.2ex] \vec{x}_P(t_0) = \vec{x}_{P0} \end{cases}](http://upload.wikimedia.org/math/b/2/a/b2a2d146a9a85282f34fe3b2f55e049e.png)
The suffix P indicates that we are following the motion of a fluid particle. Note that at point 
the curve is parallel to the flow velocity vector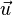 
, where the velocity vector is evaluated at the position of the particle at that time t.
Streaklines
Streaklines can be expressed as,
![\begin{cases} \displaystyle \frac{d \vec{x}_{P} }{dt} = \vec{u}_{P} (\vec{x}_{P},t) \\[1.2ex] \vec{x}_{P}( t = \tau_{P}) = \vec{x}_{P0} \end{cases}](http://upload.wikimedia.org/math/a/f/c/afcbb3fdc803a1e5ef65529d5fc8af3d.png)
where, 
is the velocity of a particle P at location 
and time t. The parameter τP, parametrizes the streakline 
and 
, where t0 is a time of interest.
No comments:
Post a Comment