Monday, February 15, 2010

Biot- Savart Law and Magnetic Field Intensity

The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant. The law is valid in the magnetostatic approximation, and results in a B field consistent with both Ampère's circuital law and Gauss's law for magnetism.

The Biot–Savart law is used to compute the magnetic field generated by a steady current, i.e. a continual flow of charges, for example through a wire, which is constant in time and in which charge is neither building up nor depleting at any point. The equation in SI units is

\mathbf{B} = \int\frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{\hat r}}{r^2},

or, equivalently,

\mathbf{B} = \int\frac{\mu_0}{4\pi} \frac{I d\mathbf{l} \times \mathbf{r}}{r^3},

where

I is the current,
dl is a vector, whose magnitude is the length of the differential element of the wire, and whose direction is the direction of conventional current,
B is the net magnetic field,
μ0 is the magnetic constant,
\scriptstyle{\hat{\mathbf{r}}} is the displacement unit vector in the direction pointing from the wire element towards the point at which the field is being computed, and
\scriptstyle{\mathbf{r}=r\hat{\mathbf{r}}} is the full displacement vector from the wire element to the point at which the field is being computed.

The symbols in boldface denote vector quantities.

To apply the equation, you choose a point in space at which you want to compute the magnetic field. Holding that point fixed, you integrate over the path of the current(s) to find the total magnetic field at that point. The application of this law implicitly relies on the superposition principle for magnetic fields, i.e. the fact that the magnetic field is a vector sum of the field created by each infinitesimal section of the wire individually.

The formulations given above work well when the current can be approximated as running through an infinitely-narrow wire. If the current has some thickness, the proper formulation of the Biot–Savart law (again in SI units) is:

\mathbf{B} = \int\frac{\mu_0}{4\pi}\ \frac{(\mathbf{J}\, dV) \times \mathbf{\hat r}}{r^2}, or (equivalently),

\mathbf{B} = \int\frac{\mu_0}{4\pi}\ \frac{(\mathbf{J}\, dV) \times \mathbf{r}}{r^3},

where dV is the differential element of volume and J is the current density vector in that volume.

The Biot–Savart law is fundamental to magnetostatics, playing a similar role to Coulomb's law in electrostatics. When magnetostatics does not apply, the Biot–Savart law should be replaced by Jefimenko's equations.

Forms

General

In the magnetostatic approximation, the magnetic field can be determined if the current density j is known:

\mathbf{B}= K_m\int{\frac{\mathbf{j} \times \mathbf{\hat r}}{r^2}dV}

where:

\ dV is the differential element of volume.
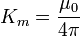K_m = \frac{\mu_0}{4\pi} is the magnetic constant

Constant uniform current

In the special case of a constant, uniform current I, the magnetic field B is

\mathbf B = K_m I \int \frac{d\mathbf l \times \mathbf{\hat r}}{r^2}

Point charge at constant velocity

In the case of a charged point particle q moving at a constant velocity v, then Maxwell's equations give the following expression for the electric field and magnetic field:

\mathbf{E} = \frac{q}{4\pi \epsilon_0} \frac{1-v^2/c^2}{(1-v^2\sin^2\theta/c^2)^{3/2}}\frac{\mathbf{\hat r}}{r^2}
\mathbf{B} = \mathbf{v} \times \frac{1}{c^2} \mathbf{E}

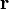where \mathbf{\hat r} is the vector pointing from the current (non-retarded) position of the particle to the point at which the field is being measured, and θ is the angle between \mathbf{v}and \mathbf{r}.

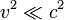When v^2 \ll c^2 , the electric field and magnetic field can be approximated as.

\mathbf{E} =\frac{q}{4\pi\epsilon_0}\ \frac{\mathbf{\hat r}}{r^2} 、
\mathbf{B} =\frac{\mu_0 q \mathbf{v}}{4\pi} \times \frac{\mathbf{\hat r}}{r^2}

These equations are called the "Biot–Savart law for a point charge" due to its closely analogous form to the "standard" Biot–Savart law given previously. These equations were first derived by Oliver Heaviside in 1888.

Magnetic fields surround magnetic materials and electric currents and are detected by the force they exert on other magnetic materials and moving electric charges. The magnetic field at any given point is specified by both a direction and a magnitude (or strength); as such it is a vector field.

For the physics of magnetic materials, see magnetism and magnet, more specifically ferromagnetism, paramagnetism, and diamagnetism. For constant magnetic fields, such as are generated by magnetic materials and steady currents, see magnetostatics. A changing magnetic field generates an electric field and a changing electric field results in a magnetic field. (See electromagnetism.) In view of special relativity, the electric and magnetic fields are two interrelated aspects of a single object, called the electromagnetic field. A pure electric field in one reference frame is observed as a combination of both an electric field and a magnetic field in a moving reference frame.

In modern physics, the magnetic (and electric) fields are understood to be due to a photon field; in the language of the Standard Model the electromagnetic force is mediated by photons. Most often this microscopic description is not needed because the simpler classical theory covered in this article is sufficient; the difference is negligible under most circumstances.

Posted by at
Labels:

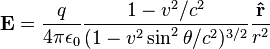
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)