ELECTROMAGNETICS: Coulombs Law

Coulomb's law is the fundamental law of the electric force between two stationary, charged particles. It has a form very similar to the universal law of gravitation. Charles Agustin de Coulomb ( 1736- 1806 ) studied the interaction of forces of charged particles in detail in 1784. He used a torsion balance ( see figure below)similar to one used 13 years later by Cavendish to study the much weaker gravitational interaction. For point charges, charged bodies that are very small comparison with the distance r between them, Coulomb found that the electric force is proportional to 1/ r². That is, when the distance r doubles, the force decreases to 1/2 of its initial value; when the distance is halved, the force increases to four times its initial value.

The electric force between two point charges also depends on the quantity of charge on each body, which we will denote by q or Q. To explore this dependence, Coulomb divided a charge into two equal parts by placing a small charged spherical conductor into contact with an identical but uncharged sphere; by symmetry, the charge is shared equally between the two spheres. ( Note the essential role of the principle of conservation of charge in this procedure.) Thus, he could obtain one half, one quarter, and so on, of any initial charge. He found out that the forces that two points charges q1 and q2 exert on each other are proportional to each charge and therefore are proportional to the product q1q2 of the two charges.

Thus, Coulomb established what we now call Coulomb's Law

The magnitude of the electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.

In mathematical terms, the magnitude F of the force that each of two pints charges q1 and q2 a distance r apart exerts on the other can be expressed as

where k is a proportionally constant whose numerical value depends on the system of unit used.

The direction of the forces the two charges exert on each other are always along the line joinong them. When the charges q1 and q2 have the same sign, either both positive or both negative, the forces are repulsive; when the charges have positive signs, the forces are attractive. The two forces obey Newtons third law; they are always equal in magnitude and opposite in direction, even when the charges are not equal.

The proportionality of the electric force to 1/r² has been verified with great precision. There is no reason to suspect that the exponent is anything different from precisely 2. Electric and gravitational interactions are two distinct classes of these phenomena. Electric interactions depend on electric charges and can be either attractive or repulsive, while gravitational interactions depend on the mass and are always attractive (because there is no such thing as negative mass).

The value of the proportionality constant k in Coulomb's law depends on the system of units used. In our study of electricity and magnetism, we will use the SI units exclusively. The SI units includes most of the familiar units such as the volt, the ampere, the ohm and the watt. (There is no British system of electric units.) The SI unit of electric charge is called one coulomb (1 C). In SI units, the constant k is
k= 8.987551787 x 10^9 Nm²

The value k is known to such large number of significant digits because this value is closely related to the speed of light in a vacuum.

Coulomb's law describes only the interaction of of two point charges. Experiment shows that when two charges exert forces simultaneously on a third charge, the total force acting on that charge is the vector sum of the forces that the two charges exert individually. This important property, called the principle of superposition of forces, holds for any number of charges. By using this principle, we can apply Coulomb's law to any collection of charges.

Strictly speaking, Coulomb's law must be used only for point charges in vacuum. If matter is present in the space between the charges, the net force acting on each charge is altered because charges are included in the molecules of the intervening material. As a practical manner, we can apply Coulomb's law unaltered for point charges in air. At normal atmospheric pressure, the presence of air changes the electric force from each vacuum value by only about one part in 2000.

Scalar form

Diagram describing the basic mechanism of Coulomb's law; like charges repel each other and opposite charges attract each other.

The scalar form of Coulomb's law will only describe the magnitude of the electrostatic force between two electric charges. If direction is required, then the vector form is required as well. The magnitude of the electrostatic force (F) on a charge (q₁) due to the presence of a second charge (q₂), is given by

$F = k_\mathrm{e} \frac{q_1q_2}{r^2}$

where r is the distance between the two charges and k_e a proportionality constant. A positive force implies a repulsive interaction, while a negative force implies an attractive interaction.

The proportionality constant k_e, called Coulomb's constant (sometimes called Coulomb's force constant) is related to the properties of space and can be calculated exactly:

$\begin{align} k_{\mathrm{e}} &= \frac{1}{4\pi\varepsilon_0} = \frac{\mu_0\ {c_0}^2}{4 \pi}= \frac{{c_0}^2}{10^7}\frac{H}{m}=\\ &= 8.987\ 551\ 787\ 368\ 176\ 4 \times 10^9 \ \mathrm{N \cdot m^2 \cdot C^{-2}}. \\ \end{align}$

By definition the speed of light in vacuum, denoted c₀, is 299,792,458 m·s⁻¹, and the magnetic constant (μ₀), is defined as 4π × 10⁻⁷ H·m⁻¹ leading to the definition for the electric constant (ε₀) as ε₀ = 1/(μ₀c) ≈ 8.854187817×10⁻¹² F·m⁻¹. In cgs units, the unit charge, esu of charge or statcoulomb, is defined so that this Coulomb force constant is 1.

This formula says that the magnitude of the force is directly proportional to the magnitude of the charges of each object and inversely proportional to the square of the distance between them. The exponent in Coulomb's Law has been found to be equal to −2 with precision of at least 2.7±3.1×10⁻¹⁶.

Coulomb's law can also be interpreted in terms of atomic units with the force expressed in Hartrees per Bohr radius, the charge in terms of the elementary charge, and the distances in terms of the Bohr radius.

Electric field

It follows from the Lorentz Force Law that the magnitude of the electric field (E) created by a single point charge (q) at a certain distance (r) is given by:

$E = {1 \over 4\pi\varepsilon_0}\frac{q}{r^2}.$

For a positive charge, the direction of the electric field points along lines directed radially away from the location of the point charge, while the direction is the opposite for a negative charge. The SI units of electric field are volts per meter or newtons per coulomb.

Vector form

In order to obtain both the magnitude and direction of the force on a charge, $q 1$ at position $\mathbf{r}_1$ , experiencing a field due to the presence of another charge, q₂ at position $\mathbf{r}_2$ , the full vector form of Coulomb's law is required.

$\mathbf{F} = {1 \over 4\pi\varepsilon_0}{q_1q_2(\mathbf{r}_1 - \mathbf{r}_2) \over |\mathbf{r}_1 - \mathbf{r}_2|^3} = {1 \over 4\pi\varepsilon_0}{q_1q_2 \over r^2}\mathbf{\hat{r}}_{21},$

where $r$ is the separation of the two charges. This is simply the scalar definition of Coulomb's law with the direction given by the unit vector, $\mathbf{\hat{r}}_{21}$ , parallel with the line from charge $q 2$ to charge $q 1$ .

If both charges have the same sign (like charges) then the product $q 1 q 2$ is positive and the direction of the force on $q 1$ is given by $\mathbf{\hat{r}}_{21}$ ; the charges repel each other. If the charges have opposite signs then the product $q 1 q 2$ is negative and the direction of the force on $q 1$ is given by $-\mathbf{\hat{r}}_{21}$ ; the charges attract each other.

System of discrete charges

The principle of linear superposition may be used to calculate the force on a small test charge, $q$ , due to a system of $N$ discrete charges:

$\mathbf{F}(\mathbf{r}) = {q \over 4\pi\varepsilon_0}\sum_{i=1}^N {q_i(\mathbf{r} - \mathbf{r}_i) \over |\mathbf{r} - \mathbf{r}_i|^3} = {q \over 4\pi\varepsilon_0}\sum_{i=1}^N {q_i \over R_i^2}\mathbf{\hat{R}}_i,$

where $q i$ and 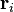$\mathbf{r}_i$ are the magnitude and position respectively of the $i t h$ charge, $\mathbf{\hat{R}}_{i}$ is a unit vector in the direction of $\mathbf{R}_{i} = \mathbf{r} - \mathbf{r}_i$ (a vector pointing from charge $q i$ to charge $q$ ), and $R i$ is the magnitude of $\mathbf{R}_{i}$ (the separation between charges $q i$ and $q$ ).

Continuous charge distribution

For a charge distribution an integral over the region containing the charge is equivalent to an infinite summation, treating each infinitesimal element of space as a point charge $d q$ .

For a linear charge distribution (a good approximation for charge in a wire) where $\lambda(\mathbf{r^\prime})$ gives the charge per unit length at position $\mathbf{r^\prime}$ , and $dl^\prime$ is an infinitesimal element of length,

$dq = \lambda(\mathbf{r^\prime})dl^\prime$ .

For a surface charge distribution (a good approximation for charge on a plate in a parallel plate capacitor) where $\sigma(\mathbf{r^\prime})$ gives the charge per unit area at position $\mathbf{r^\prime}$ , and $dA^\prime$ is an infinitesimal element of area,

$dq = \sigma(\mathbf{r^\prime})\,dA^\prime.\,$

For a volume charge distribution (such as charge within a bulk metal) where $\rho(\mathbf{r^\prime})$ gives the charge per unit volume at position $\mathbf{r^\prime}$ , and $dV^\prime$ is an infinitesimal element of volume,

$dq = \rho(\mathbf{r^\prime})\,dV^\prime.$

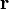The force on a small test charge $q^\prime$ at position $\mathbf{r}$ is given by

$\mathbf{F} = {q^\prime \over 4\pi\varepsilon_0}\int dq {\mathbf{r} - \mathbf{r^\prime} \over |\mathbf{r} - \mathbf{r^\prime}|^3}.$

Graphical representation

Below is a graphical representation of Coulomb's law, when $q 1 q 2 > 0$ . The vector $\mathbf{F}_1$ is the force experienced by $q 1$ . The vector $\mathbf{F}_2$ is the force experienced by $q 2$ . Their magnitudes will always be equal. The vector $\mathbf{r}_{21}$ is the displacement vector between two charges ( $q 1$ and $q 2$ ).

A graphical representation of Coulomb's law.

Electrostatic approximation

In either formulation, Coulomb’s law is fully accurate only when the objects are stationary, and remains approximately correct only for slow movement. These conditions are collectively known as the electrostatic approximation. When movement takes place, magnetic fields are produced which alter the force on the two objects. The magnetic interaction between moving charges may be thought of as a manifestation of the force from the electrostatic field but with Einstein’s theory of relativity taken into consideration.

PROBLEM SOLVING STRATEGY

1. As always, consistent units are essential. With the value 0f k given above, distances must be in meters, charge in coulombs, and force in newtons. If you are given distances in centimeters, inches or furlongs, don't forget to convert! When a charge is given in microcoulombs or nanocoloumbs, remember that ....

2. Remember that the electric force, like any force, is a vector. When the forces acting on a charge are caused by two or more other charges, the total force on the charge is the vector sum of the individual forces. It's often useful to use components in an xy- coordinate system. Be sure to use correct vector notation; if a symbol represents a vector quantity, put an arrow above it. If you get sloppy with your notations, you will also get sloppy with your thinking.

3. Some examples and problems in this and other topics involve a continuous distribution of charge along a line or over a surface. In these cases the vector sum described in Step 2 becomes a vector integral, usually carried out by use of components. we divide the total charge distribution into infinitesimal pieces, use Coulomb's law for each piece, and then integrate to find the vector sum. Sometimes, this

ELECTROMAGNETICS

Monday, February 15, 2010

Coulombs Law

Scalar form

Electric field

Vector form

System of discrete charges

Continuous charge distribution

Graphical representation

Electrostatic approximation

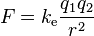
No comments:

Post a Comment

Blog Archive

About Me