

In physics, an electric field is a field of force with a field strength equal to the force per unit charge at that point. Basically, it is a field in which a charge experiences a force. The concept of an electric field was introduced by Michael Faraday.
The electric field is a with volts units of newtons per coulomb (N C−1) or, equivalently, volts per meter (V m−1). The SI base units of the electric field are kg·m·s−3·A−1. The strength of the field at a given point is defined as the force that would be exerted on a positive test charge of +1 coulomb placed at that point; the direction of the field is given by the direction of that force. Electric fields contain electrical energy with energy density proportional to the square of the field amplitude. The electric field is to charge as gravitational acceleration is to mass and force density is to volume.
An electric field that changes with time (such as due to the motion of charged particles in the field) will also influence the magnetic field of that region of space. Thus, in general, the electric and magnetic fields are not completely separate phenomena; what one observer perceives as an electric field, another observer in a different frame of reference perceives as a mixture of electric and magnetic fields. For this reason, one speaks of "electromagnetism" or "electromagnetic fields." In quantum mechanics, disturbances in the electromagnetic fields are called photons, and the energy of photons is quantized.
The electric field is defined as the force per unit charge that would be experienced by a stationary point charge at a given location in the field:
where
Taken literally, this equation only defines the electric field at the places where there are stationary charges present to experience it. Furthermore, the force exerted by another charge q will alter the source distribution, which means the electric field in the presence of q differs from itself in the absence of q. However, the electric field of a given source distribution remains defined in the absence of any charges with which to interact. This is achieved by measuring the force exerted on successively smaller test charges placed in the vicinity of the source distribution. By this process, the electric field created by a given source distribution is defined as the limit as the test charge approaches zero of the force per unit charge exerted thereupon.
This allows the electric field to be dependent on the source distribution alone.
As is clear from the definition, the direction of the electric field is the same as the direction of the force it would exert on a positively-charged particle, and opposite the direction of the force on a negatively-charged particle. Since like charges repel and opposites attract (as quantified below), the electric field tends to point away from positive charges and towards negative charges.
Based on Coulomb's Law for interacting point charges, the contribution to the E-field at a point in space due to a single, discrete charge located at another point in space is given by the following:
where
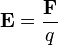
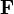 is the force acting on the charge.
is the force acting on the charge.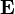 is the magnitude of the electric field.
is the magnitude of the electric field.

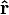 is the unit vector
is the unit vector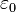 is the electric constant.
is the electric constant.
No comments:
Post a Comment